Insertion Sort

Wiki pic - Graphical example of insertion sort. Source.

Iterative Insertion Sort

function insertionSortIterative(arr) {
	const len = arr.length

	for (let i = 1; i < len; i++) {
		const ith = arr[i]
		let j = i - 1

		while (j >= 0 && arr[j] > ith) {
			arr[j + 1] = arr[j]
			j--
		}

		arr[j + 1] = ith
	}

	return
}

/*
Time Complexity:
Average and Worse Case: O(n^2)
Best Case: O(n)
Space complexity - O(1)
*/

/* ---------------------------------------------------------------------------- */

const testCases = [
	[
		[5, 4, 3, 2, 1],
		[1, 2, 3, 4, 5],
	],
	[
		[5, 6, 1, 0, 6, 2],
		[0, 1, 2, 5, 6, 6],
	],
	[
		[-1, 6, 2, 100, 0, -11],
		[-11, -1, 0, 2, 6, 100],
	],
]

for (const test of testCases) {
	insertionSortIterative(test[0])
	console.log(JSON.stringify(test[0]) === JSON.stringify(test[1]))
}

Recursive Insertion Sort

// Recursive insertion sort with shifting of elements.
function insertionSortRecursive(arr) {
	const lastIndex = arr.length - 1

	function recurse(n) {
		if (n <= 0) return

		recurse(n - 1)

		// Hold the value to be inserted in nth
		const nth = arr[n]

		// Starting at n - 1, until arr[j] < nth, keep shifting arr[j] to the right
		let j = n - 1

		while (j >= 0 && arr[j] > nth) {
			arr[j + 1] = arr[j]
			j--
		}

		// Place nth in correct position
		arr[j + 1] = nth

		return
	}

	recurse(lastIndex)

	return
}

/*
Time Complexity:
Average and Worse Case: O(n^2)
Best Case: O(n)
Space complexity - O(n) (stack size)
*/

/* ---------------------------------------------------------------------------- */

const testCases = [
	[
		[5, 4, 3, 2, 1],
		[1, 2, 3, 4, 5],
	],
	[
		[5, 6, 1, 0, 6, 2],
		[0, 1, 2, 5, 6, 6],
	],
	[
		[-1, 6, 2, 100, 0, -11],
		[-11, -1, 0, 2, 6, 100],
	],
]

for (const test of testCases) {
	insertionSortRecursive(test[0])
	console.log(JSON.stringify(test[0]) === JSON.stringify(test[1]))
}

Calculating the Time Complexity of Recursive Insertion Sort

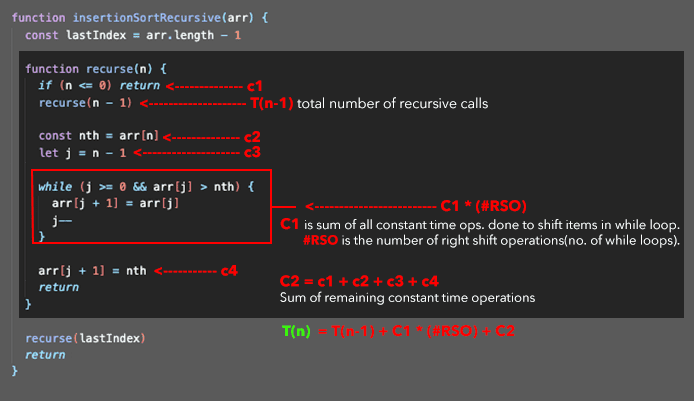
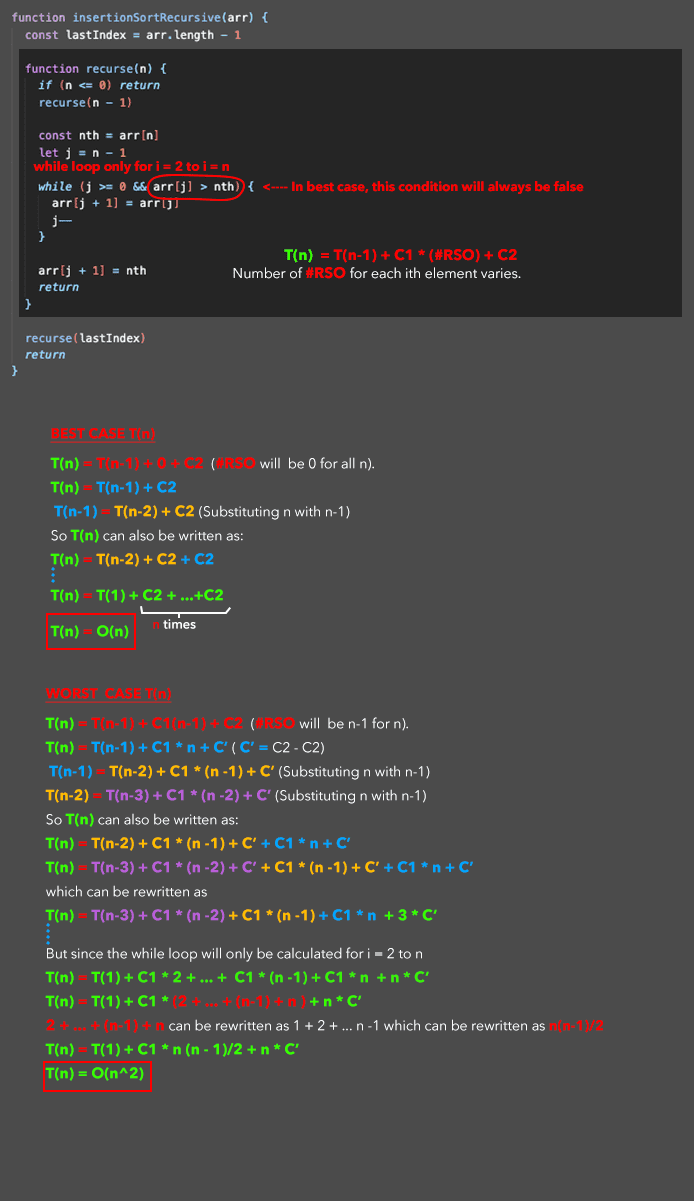
There is another way to implement recursive insertion sort - with repeated swaps to 'bubble up' the nth element.

function insertionSortRecursiveBubble(arr) {
	const lastIndex = arr.length - 1

	function recurse(n) {
		// base case
		if (n <= 0) return
		// recurse on n - 1
		recurse(n - 1)
		// Bubble up and insert nth item in its place
		let j = n
		while (j >= 1 && arr[j - 1] > arr[j]) {
			swap(arr, j - 1, j)
			j--
		}
		return
	}

	recurse(lastIndex)
	return
}

function swap(array, i, j) {
	let temp = array[i]
	array[i] = array[j]
	array[j] = temp
}