Heap Sort

Wiki pic - Graphical example of heap sort. Source.

In-place heap sort:

Given an unsorted array,

1. Build a max heap in place using buildMaxHeap function.
2. Loop through the items of the heap.
3. Instead of extracting and removing the max from the heap, swap it with last item of the heap and decrement heap size.
4. "Heapify" or sink down the swapped item which is at index 0.

/*
Time Complexity = Time to build heap + Time to heapify n items 
T = O(n) + O(n * logn)
Since O(nlogn) > O(n), dropping O(n)
T = O(nlogn)

Space complexity - O(1) (Since heapify isn't recursive)
*/
function heapSort(arr) {
	// O(n)
	buildMaxHeap(arr)
	let lastHeapIndex = arr.length - 1

	// n items so T is O(n * logn)
	while (lastHeapIndex > 0) {
		swap(arr, 0, lastHeapIndex)
		lastHeapIndex--
		heapify(arr, 0, lastHeapIndex) // O(logn)
	}
}

// Time Complexity of buildMaxHeap O(n). It builds the max heap in place.
function buildMaxHeap(arr) {
	// start at rightmost node which is not a leaf
	let i = Math.floor(arr.length / 2 - 1)
	const lastIndex = arr.length - 1

	while (i >= 0) {
		heapify(arr, i, lastIndex)
		i--
	}
}

// Time Complexity of heapify - O(log n)
function heapify(heap, p, lastIndex) {
	while (p < lastIndex) {
		const r = 2 * p + 2,
			l = r - 1,
			right = heap[r],
			left = heap[l]

		let swapIndex = null,
			max = heap[p]

		if (l <= lastIndex && left > max) {
			swapIndex = l
			max = left
		}

		if (r <= lastIndex && right > max) {
			swapIndex = r
		}

		if (swapIndex === null) break
		swap(heap, p, swapIndex)
		p = swapIndex
	}
}

function swap(array, i, j) {
	let temp = array[i]
	array[i] = array[j]
	array[j] = temp
}

Explanation for time complexity of buildMaxHeap and why it is O(n):

/* 
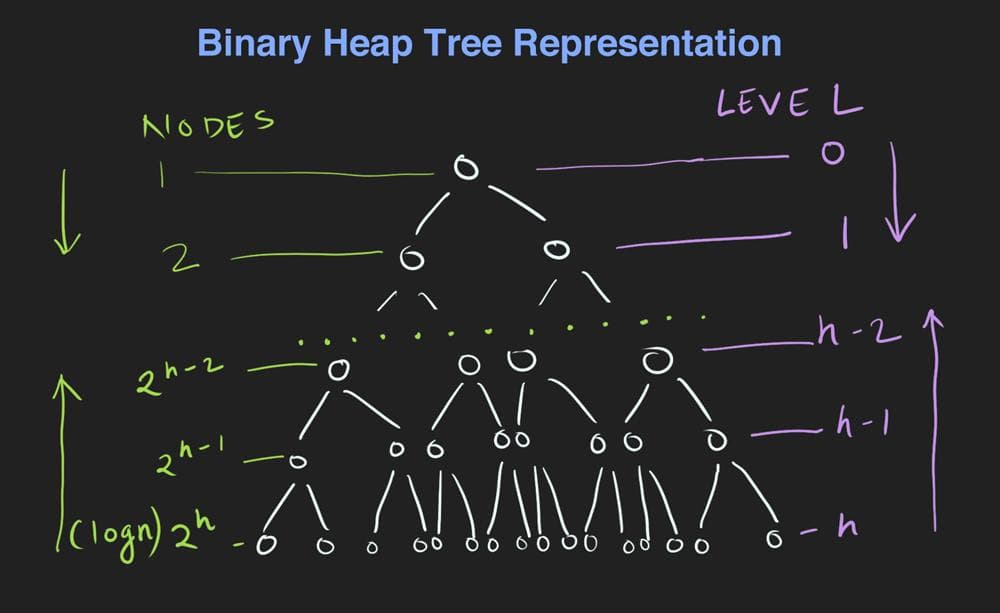
Time Complexity of building a max heap in place is O(n).
This is because of the structure of a binary heap.

| no. of nodes | Level | height - level | work done to sink down nodes | % of tree nodes |
| ------------ | ----- | -------------- | ---------------------------- | --------------- |
| 1            | 0     | h              | 1 * h                        | ...             |
| 2            | 1     | h - 1          | 2 * h-1                      | ...             |
...
| 2^h-2        | h-2   | 2              | 2^h-2 * 2                    | 12.5%           |
| 2^h-1        | h-1   | 1              | 2^h-1 * 1                    | 25%             |
| 2^h          | h     | 0              | 2^h * 0                      | 50%             |

                                         T(n) = sum of this column

T(n) = sum of this column
T(n) = 2^h * 0 + 2^h-1 * 1 + 2^h-2 * 2 + ... + 2 * h-1 + 1 * h
                                                             |
height of tree = log(n), so we can replace the last h with log(n)

T(n) = 2^h * 0 + 2^h-1 * 1 + 2^h-2 * 2 + ... + 2 * h-1 + 1 * log(n)

Subbing out the log(n) with ∞, we can say that T(n) of n items <= T(n) of ∞ items
*/

Rewriting and solving the equation, we get:

Link to wiki on arithmetico-geometric series.

If you look at the table and the percentages of number of nodes per level, you'll notice that 87.5% of nodes are in the last three levels which don't need much work and 50% of nodes don't need any work at all to sink down. So O(n) isn't really that surprising.

Heap sort with O(n) auxiliary space:

Given an unsorted array,

1. Create a min heap using MinBinaryHeap data structure.
2. Loop through array items and insert each item into the min heap.
3. Initialize an empty auxiliary array to hold sorted values.
4. Until there are items in the heap, keep extracting min from the min heap and pushing it into the sorted array.

Link to Binary Heap

const { MinBinaryHeap } = require('../utils')

function heapSort(arr) {
	const minHeap = new MinBinaryHeap(),
		sorted = []
	// n items
	for (const item of arr) {
		minHeap.insert(item) // O(logn)
	}

	// n items
	while (minHeap.size > 0) {
		const min = minHeap.extractMin() // O(logn)
		sorted.push(min)
	}

	return sorted
}

/*
Time Complexity - O(nlogn) (inserting n items into heap) + O(nlogn) (extracting n items from heap)
T = O(nlogn)
Space complexity - O(n) auxillary space (for sorted array and heap)
*/

/* ---------------------------------------------------------------------------- */

// Tests
const testCases = [
	[
		[5, 6, 1, 0, 6, 2],
		[0, 1, 2, 5, 6, 6],
	],
	[
		[-1, 6, 2, 100, 0, -11],
		[-11, -1, 0, 2, 6, 100],
	],
	[
		[7, 6, 5, 4, 3, 2, 1, 0],
		[0, 1, 2, 3, 4, 5, 6, 7],
	],
]

for (const test of testCases) {
	const sorted = heapSort(test[0])
	console.log(sorted)
	console.log(JSON.stringify(sorted) === JSON.stringify(test[1]))
}